Archive
컴퓨터구조 1-7주차 본문
728x90
메가존아이티평생교육원 컴퓨터구조 참고
컴퓨터시스템의 구성
- 하드웨어
- 5대 기능: input(입력), process(연산, 제어), storage(저장), output(출력)
- 중앙처리장치 CPU central processing unit
- 연산장치 ALU arithmetic logic unit
- 산술연산과 논리연산을 수행하는 계산기
- 산술연산: 사칙연산
- 논리연산: 참과 거짓을 판별하는 연산
- 산술연산과 논리연산을 수행하는 계산기
- 제어장치 CU control unit
- CPU 내부에서 일어나는 모든 작업을 통제 및 관리하는 지휘자
- 명령어를 해석하고, 필요한 곳으로 제어 신호를 전달함
- 레지스터 register
- CPU가 데이터를 처리할 때 사용하는 빠르고 임시적인 작업 공간
- 연산장치 ALU arithmetic logic unit
- 기억장치 memory device
- 주기억장치 main memory = RAM random access memory
- CPU가 직접 데이터를 가져와 처리하는 공간
- 프로그램이 실행될 때 필요한 데이터와 명령어가 여기에 올라옴!
- 보조기억장치 secondary memory
- 데이터와 프로그램을 영구적으로 저장하는 공간
- CPU와 직접 소통이 불가하기 때문에, CPU를 통해 해결해야 하는 일이 있다면 활용할 데이터를 주기억장치로 옮긴 후 처리해야 함
- 예) 자기 테이프, 자기 디스크, 자기 드럼, 플로피 디스크, 하드 디스크 ...
- 주기억장치 main memory = RAM random access memory
- 입출력장치
- 입력장치 input device
- 출력장치 output device
- 소프트웨어
- 시스템 소프트웨어 system software
- 여러 컴퓨터 시스템에서 공통적으로 필요한 프로그램
- 운영체제 OS operating system
- 컴파일러
- 입출력 제어 프로그램
- 여러 컴퓨터 시스템에서 공통적으로 필요한 프로그램
- 응용 소프트웨어 application software
- 특정한 응용 분야에서 특수 목적을 위해 사용하는 프로그램
- 예) 사무 자동화 프로그램 OA, 인터넷 웹 브라우저
- 시스템 소프트웨어 system software
컴퓨터의 분류
- 사용 목적에 따른 분류
- 전용 컴퓨터 special purpose computer
- 특정 목적을 위해 만들어진 컴퓨터
- 예) 군사용 컴퓨터
- 범용 컴퓨터 general purpose computer
- 다양한 목적에 활용 가능한 컴퓨터
- 전용 컴퓨터 special purpose computer
- 사용 데이터에 따른 분류
- 아날로그 컴퓨터
- 온도, 압력처럼 연속적인 데이터를 처리함
- 디지털 컴퓨터
- 0과 1, 불연속적인 데이터를 처리함
- 하이브리드 컴퓨터
- 아날로그와 디지털의 장점을 취해, 어떤 종류의 데이터도 처리 가능
- 아날로그 컴퓨터
- 처리 능력에 따른 분류
- 마이크로 컴퓨터 micro computer
- 마이크로 프로세서를 사용
- 주로 개인이 사용
- 예) desk-top, lap-top, palm-top, personal digital assistant, smart phone, tablet PC
- < 워크스테이션 workstation
- 주로 UNIX 계열의 운영체제 사용
- 주로 전문적인 작업(그래픽, 공학 설계 등)에 사용
- 대형 컴퓨터나 슈퍼 컴퓨터와 연결하여 업무 처리
- < 중형 컴퓨터 mini computer
- 주로 기업이나 단체의 부서 단위에서 사용
- < 대형 컴퓨터 mainframe computer
- 다수의 단말기를 연결해 온라인 업무나 분산 처리 업무에 사용
- < 슈퍼 컴퓨터 super computer
- 원자력 개발, 항공우주, 기상 예측 분야에서 사용
- 마이크로 컴퓨터 micro computer
- 구조에 따른 분류
- 파이프라인 슈퍼 컴퓨터 pipeline super computer
- 하나의 CPU 내에 다수의 연산장치를 포함
- 각 연산장치는 파이프 라이닝 구조로 고속 벡터 계산 가능
- 대규모 병렬 컴퓨터 massively parallel computer
- 하나의 시스템 내에 상호 연결된 수백 혹은 수천 개 이상의 프로세스들을 포함
- 프로세서들이 하나의 작업을 나누어서 병렬로 처리하는 구조
- 파이프라인 슈퍼 컴퓨터 pipeline super computer
정보의 표현
- 단위
- 비트 bit
- 컴퓨터에서 사용하는 최소 단위
- 0 또는 1
- 니블 nibble = 4bit
- 바이트 byte = 8bit
- 의미를 갖는 최소 단위
- 저장장치의 용량 단위
- byte(B), kilo byte(KB), mega byte(MB), giga byte(GB), tera byte(TB) → 1024배씩 커짐
- 워드 word = 주로 32bit
- 컴퓨터가 한 번에 처리할 수 있는 최소 단위
- 컴퓨터 종류에 따라
- half word: word = 16bit
- full word: word = 32bit
- 수의 진법
- 10진법 decimal notation
- 10진수의 한 자리는 최소 4bit가 있어야 표현 가능 (하지만 9가 한 자리를 차지하는 가장 큰 수인 만큼, 4bit를 효율적으로 사용하지 못함)
- 2진법 binary notation
- 8진법 octal notation
- 16진법 hexademical notation
- 진법 변환 방법 ★
- 10진법 decimal notation
- 비트 bit

- 데이터의 2진수 표현
- 부호화-크기 표현 방식
- 최상위 비트로 부호를 표현: 0은 양수, 1은 음수
- 나머지 비트로 수의 절대 크기를 표현
- 한계점: 0을 표현하는 방법이 두 가지 (∵ 0은 음수로도 양수로도 표현 가능하기 때문)
- 1의 보수 표현 방식
- 음수인 경우에는 모든 비트들을 반전
- 한계점: 0을 표현하는 방법이 두 가지 (∵ 0은 음수로도 양수로도 표현 가능하기 때문)
- 2의 보수 표현 방식
- 음수인 경우에는 모든 비트들을 반전하고 1을 더함
- 2의 보수로 표현된 음수를 10진수로 변환하려면 똑같이 → 모든 비트들을 반전하고 1을 더함, 마지막에 음수 부호 붙여주면 됨!
- 음수는 항상 첫 비트가 1
- ★ n개의 비트로 나타낼 수 있는 숫자는 2^n개! -2^(n-1) ~ 2^(n-1) - 1
- 부호화-크기 표현 방식
- 비트 확장 bit extension
- 부호화-크기 표현의 비트 확장
- 부호 비트를 확장되는 최상위 자리로 이동시키고, 나머지 새로 확장되는 크기 비트들은 0으로 채움
- 예) 8bit를 16bit로 비트 확장하는 경우, 00010101 → 0000000000010101
- 2의 보수 표현의 비트 확장
- 확장되는 상위 비트들을 부호 비트와 동일한 값으로 채움
- 예) 8bit를 16bit로 비트 확장하는 경우, 11101011 → 1111111111101011
- 부호화-크기 표현의 비트 확장
보수
- 보수 complementary number
- 음수를 표현하는 데에 활용
- n 진법에서는
- n-1의 보수와 n의 보수(진보수)가 있음
- 예) 10진법에서는 9의 보수와 10의 보수가 있다.
- n-1의 보수: 둘을 더해 각 자리가 n-1이 되도록
- 예) 10진수 237에 대한 9의 보수는 999-237=762
- n의 보수: 둘을 더해 각 자리마다 자리올림이 발생하도록
- 예) 10진수 237에 대한 10의 보수는 1000-237=763
- n의 보수 = n-1의 보수 + 1
- n-1의 보수와 n의 보수(진보수)가 있음
2진수의 산술연산

- 문제
- 오버플로우 상태: 연산 결과가 표현할 수 있는 범위를 초과하여 결과값이 틀리게 되는 상태
- 특시 소수 계산 시,
- 지수 오버플로우 exponent overflow: 양의 지수값이 최대 지수값을 초과하는 오류
- 지수 언더플로우 exponent underflow: 음의 지수값이 최대 지수값을 초과하는 오류
- 가수 오버플로우 mantissa overflow: 같은 부호를 가진 두 가수들을 덧셈했을 때 올림수가 발생하는 경우
- 재조정 realignment 과정을 통해 정규화로 해결
- 가수 언더플로우 mantissa underflow: 가수의 소수점 위치 조정 과정에서 비트들이 가수의 우측 편으로 넘치는 경우
- 반올림 rounding으로 해결
논리 연산
- 논리 연산: 주어진 명제에 대해서 참 또는 거짓을 결정하는 연산
- 기본 논리 연산
- AND, OR, NOT, XOR (입력이 모두 동일한 경우에만 0을 출력하고, 나머지 경우에는 1을 출력)
- 응용 논리 연산
- 마스크 mask 연산: 원하는 위치의 비트들을 선택적으로 0으로 clear한 mask와 AND 연산을 수행
- 선택적-세트 selective-set 연산: 원하는 위치의 비트들을 선택적으로 1로 설정 후 OR 연산을 수행
- 선택적-보수 연산: 원하는 위치의 비트들을 선택적으로 1로 설정 후 XOR 연산을 수행
- 특정 위치에 있는 비트들을 반전시키고 싶을 때 활용!
- 삽입 연산: 마스크 연산과 선택적-세트 연산을 순차적으로 수행
- 특정 위치에 새로운 비트 값을 삽입하고 싶을 때 활용!
- 비교 연산: XOR 연산을 활용해 구현, 결과가 모두 0이면 두 데이터가 동일하다는 뜻
- 순환 이동 rotate shift 연산: 최상위 또는 최하위에 있는 비트가 반대편 끝에 있는 비트 위치로 이동해서 비트가 회전함
- 순환 좌측-이동 circular shift-left: 최상위 비트가 최하위 비트 위치로 이동
- 순환 우측-이동 circular shift-right: 최하위 비트가 최상위 비트 위치로 이동
- 산술적 이동 arithmetic shift 연산: 부호 비트는 유지하고, 수의 크기를 나타내는 비트들만 이동
- 회전 아니고 이동임!
- 산술적 좌측-이동
- 비는 공간은 0으로 채움
- 10진수로 변환해보면 원래 수의 두 배가 나옴
- 산술적 우측-이동
- 비는 공간은 부호 비트와 같은 숫자로 채움
- 10진수로 변환해보면 원래 수의 반이 나옴
- 따라서 좌측으로 한 비트씩 이동시킬 때마다 두 배를 한 것과 같은 결과가 나옴
- 논리적 이동 logical shift 연산: 주로 부호가 없는 데이터에 사용, 부호 비트와 상관없이 비트를 이동
- 회전 아니고 이동!
- 논리적 좌측-이동
- 비는 공간은 0으로 채움
- 논리적 우측-이동
- 비는 공간은 0으로 채움
코드
- 영숫자 코드 alphanumeric code
- 영문자와 숫자, 특수문자 데이터를 0과 1의 조합으로 구성된 코드로 표현한 것
- 예) 표준 BCD 코드, ASCII 코드, EBCDIC 코드, 유니코드 unicode
- BCD binary coded decimal

- 가중치 코드
- 8421 코드
- 각 자리에 대한 가중치가 8, 4, 2, 1
- 예) 9 → 1001
- 2421 코드
- 각 자리에 대한 가중치가 2, 4, 2, 1
- 코드의 1의 보수가 10진수의 9의 보수와 같은 자기 보수 코드!
- 예) 2에 대한 9의 보수는 7인데, 2는 0010이고 7은 1101이므로, 둘이 1의 보수 관계 있음
- 2-5진 bi-quinary 코드 = 5043210 코드
- 각 자리에 대한 가중치가 5, 0, 4, 3, 2, 1, 0
- 7개 비트 중 1은 반드시 2개여야 함, 따라서 1의 개수가 1개 이하 혹은 3개 이상인 경우 오류가 있음을 검출할 수 있음
- 예) 0 → 0100001
- 링 카운터 코드 ring counter code
- 각 자리에 대한 가중치가 9, 8, 7, 6, 5, 4, 3, 2, 1, 0
- 직관적이고 쉽지만, 메모리 낭비가 심해서 자주 사용하진 않음
- 8421 코드
- 비가중치 코드
- 3초과 코드 excess-3 code
- 해당 숫자에 3을 더하고, 2진수로 변환
- 코드의 1의 보수가 10진수의 9의 보수와 같은 자기 보수 코드!
- 예) 2에 대한 9의 보수는 7인데, 2는 0101이고 7은 1010이므로, 둘이 1의 보수 관계 있음
- 그레이 코드 gray code
- 한 비트의 변화만으로 다음 값을 만들어낼 수 있어 속도가 빠름
- 따라서 입출력 장치의 동작이나, 아날로그 신호 ↔ 디지털 신호 변환할 때 주로 사용함
- 한 비트의 변화만으로 다음 값을 만들어낼 수 있어 속도가 빠름
- 3초과 코드 excess-3 code

- 에러 검출 코드
- 패리티 코드 parity code
- 가장 간단하지만, 1비트 오류만 체크할 수 있음
- 10진수를 2진수로 변환한 것에, 패리티 코드 하나가 추가된 것
- 예) 3 → 0011 (홀수 패리티 코드) 1
- 홀수 패리티 코드: 1의 개수가 홀수가 되도록
- 짝수 패리티 코드: 1의 개수가 짝수가 되도록
- 해밍 코드 hamming code
- 에러 체크 뿐만 아니라 수정까지도 가능함, 다만 체크 비트로 활용할 3 비트가 요구됨
- 패리티 코드 parity code

기본 게이트
- 게이트 gate
- 2진 정보 (0과 1)를 처리하는 논리회로
- 표현 방법
- 기호로
- 부울 대수로
- 진리표로
- 종류: AND, OR, XOR, NOT, NAND, NOR, XNOR

- 범용 논리 게이트 universal gate
- NAND 게이트와 NOR 게이트가 해당됨
- 두 종류의 게이트를 가지고 디지털 시스템에서 사용되는 모든 게이트를 구성할 수 있음!
부울 대수
- 부울 대수 boole
- 복잡한 논리회로를 간단하게 표현하는 데에 유용한 논리대수
- 논리회로를 직접 간소화하는 것은 어렵기 때문에 → 논리 회로를 논리식으로 표현한 후, 부울대수의 기본 규칙을 활용해 간소화
- 부울대수의 변수는 0과 1 중 한 값을 가짐
- 부울함수: 부울대수와 기본연산을 활용
- 부울보수: 2진 변수의 값을 반전시키는 단항 연산자
- 복잡한 논리회로를 간단하게 표현하는 데에 유용한 논리대수
- 기본 연산 법칙
- 교환법칙 commutative law 성립
- 결합법칙 associative law 모두 다 같은 종류의 논리 연산이라면 성립
- 분배법칙 distributive law 성립
- 예) A(B+C) = AB + AC, A + (BC) = (A + B)(A + C)
- 다중부정 성립 - 두번 연속된 논리 부정은 긍정
- 드모르간의 법칙 de morgan
- 논리합 전체를 부정하면 각각 부정한 것을 논리곱한 것과 같음
- 논리곱 전체를 부정하면 각각 부정한 것을 논리합한 것과 같음
- 부울 함수의 간략화 방법 - 카르노맵 karnaugh map

R-S 플립플롭, 래치
- 래치 latch
- 입력이 변하는 즉시 출력이 변하는 메모리 소자 = 입력이 유지되는 동안 출력도 그대로 유지됨
- R-S 래치
- 가장 간단한 래치
- 두 개의 입력 단자 S set와 R reset을 가지고 있음
- S에 신호가 들어오면 출력 Q가 1로 설정됨
- R에 신호가 들어오면 출력 Q가 0으로 재설정됨
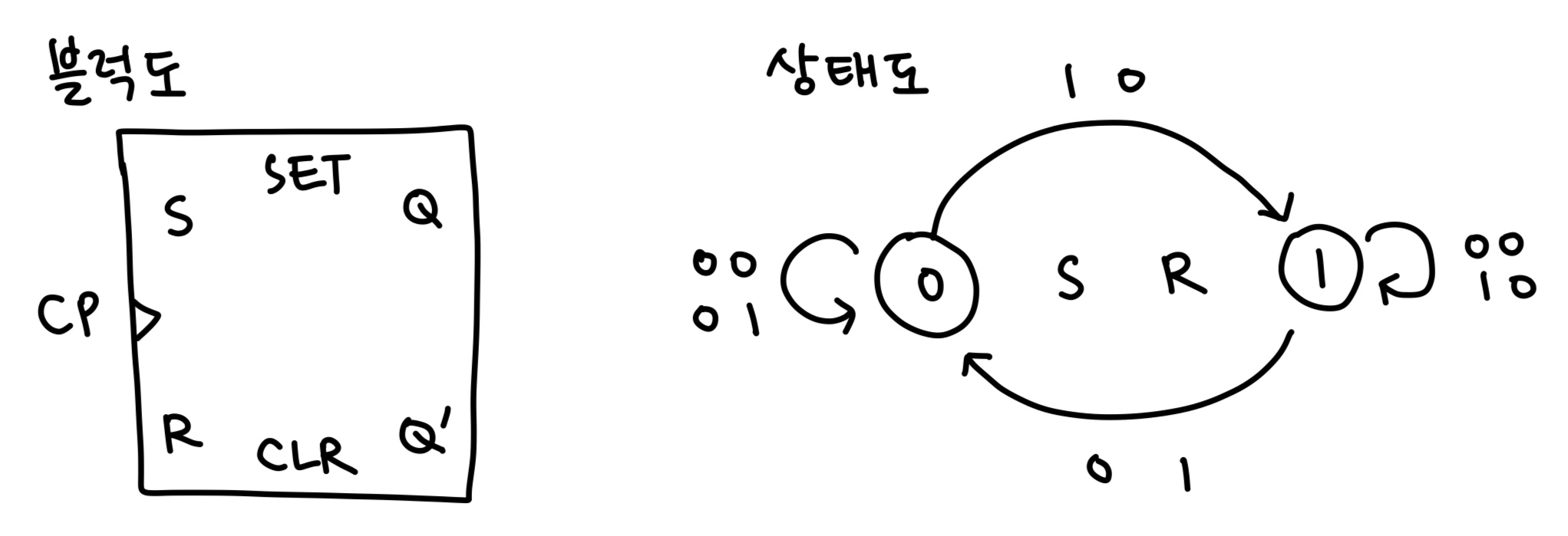
- S와 R에 모두 신호가 없으면 이전 상태를 그대로 유지함
- S와 R에 모두 신호가 있으면 불능
- 출력 Q와 Q’는 항상 보수의 상태가 되어야 하는데, S와 R에 모두 신호를 주면 출력 Q와 Q’ 모두 0이 되기 때문

| S | R | Q | Q' |
| 0 | 0 | 불변 | 불변 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 불능 | 불능 |
- 플립플롭 flip-flop
- 1 비트의 정보를 기억할 수 있는 회로
- 휘발성 = 전원이 있을 때만 기억이 유지됨
- 특정 신호가 들어올 때만 출력이 변함
- 클록 clock 신호가 높아지거나 낮아질 때와 같은 아주 짧은 특정 순간에만 입력 신호를 받아들임
- 그 외의 시간에는 아무리 입력이 변해도 출력은 그대로 유지됨
- R-S 래치를 활용해서 구현함
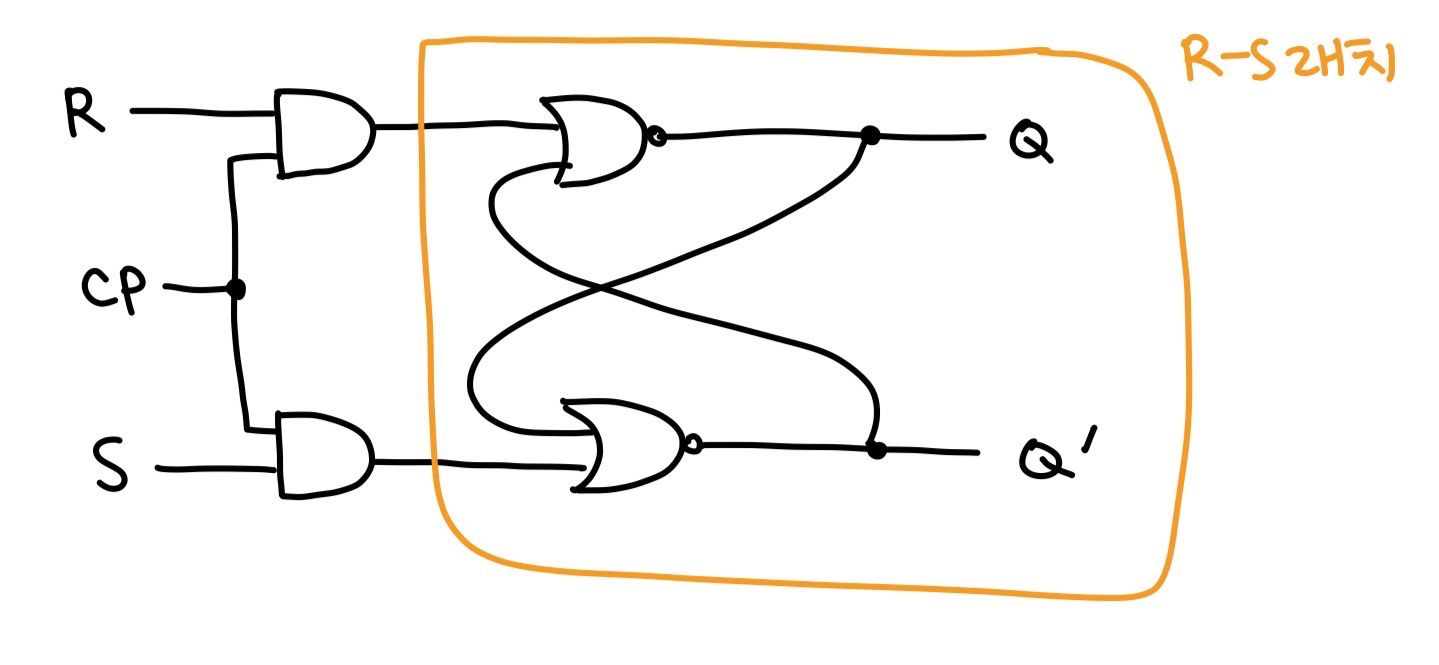
| CP | R | S | Q |
| 1 | 0 | 0 | 불변 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 불능 |
| 0 | 0 |
D 플립플롭
- R-S 플립플롭은 S와 R에 동시에 신호를 주면, 출력이 불안정한 상태가 됨 → 이 문제를 해결하기 위해 → D 플립플롭은 단 하나의 입력 데이터만 사용함
- R-S 플립플롭의 S 입력에는 D를 연결하고, R 입력에는 D’을 연결함
- 이런 구조 덕분에 두 입력이 절대로 동시에 1이 될 수 없음
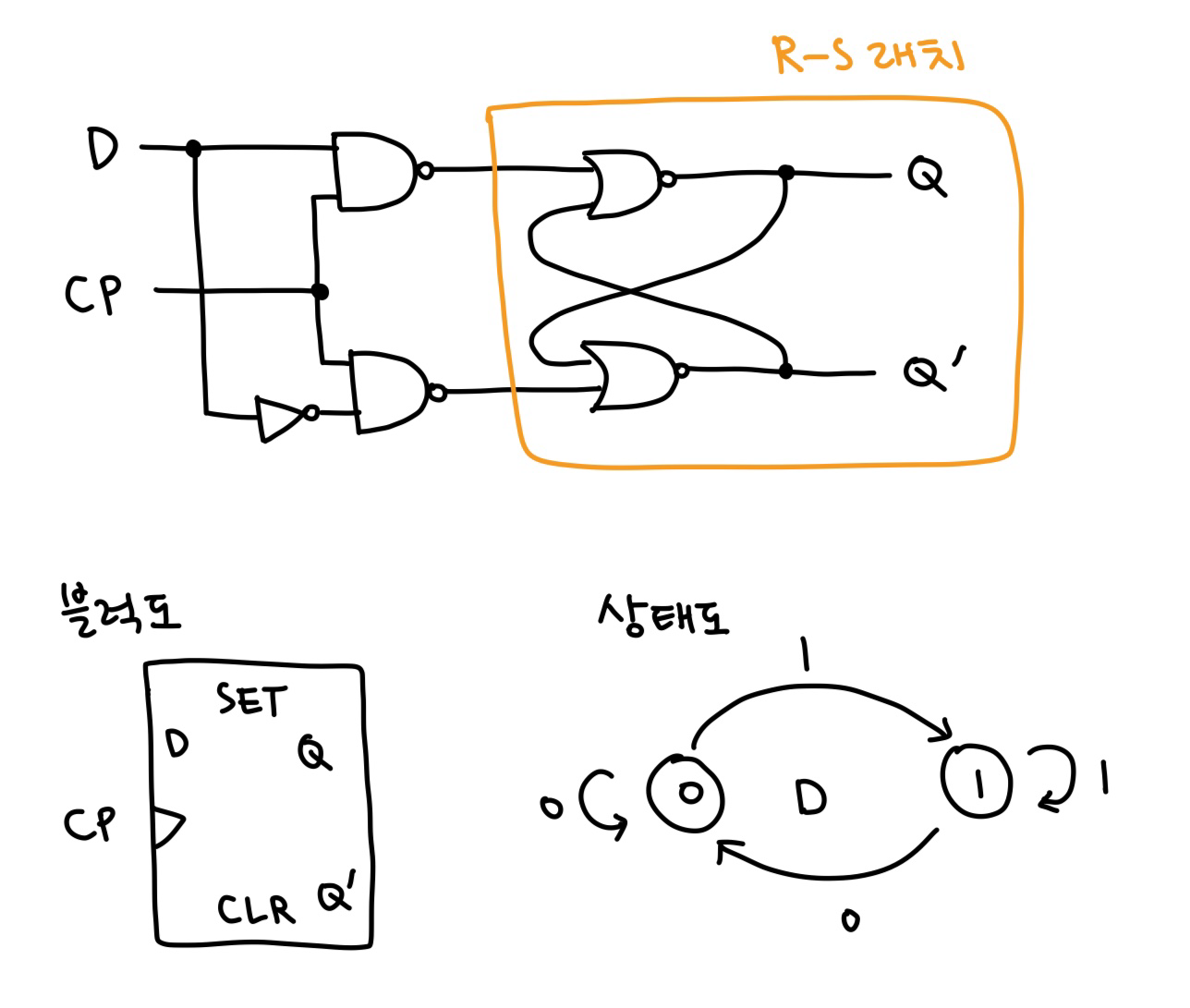
| CP | D | Q |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 0 | 0 |
J-K 플립플롭
- R-S 플립플롭은 S와 R에 동시에 신호를 주면, 출력이 불안정한 상태가 됨 → 이 문제를 해결하기 위해 → 입력에 피드백 경로를 추가하여 S와 R이 동시에 1이 되는 것을 방지하고 반전 기능으로 활용함
- R-S 플립플롭의 S는 J로, R은 K로 대응됨

| CPㅠ | J | K | Q |
| 1 | 0 | 0 | 불변 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 반전 |
| 0 | 0 |
T 플립플롭
- J-K 플립플롭의 J와 K 입력을 묶어서 하나의 입력 신호 T로 동작시키는 플립플롭
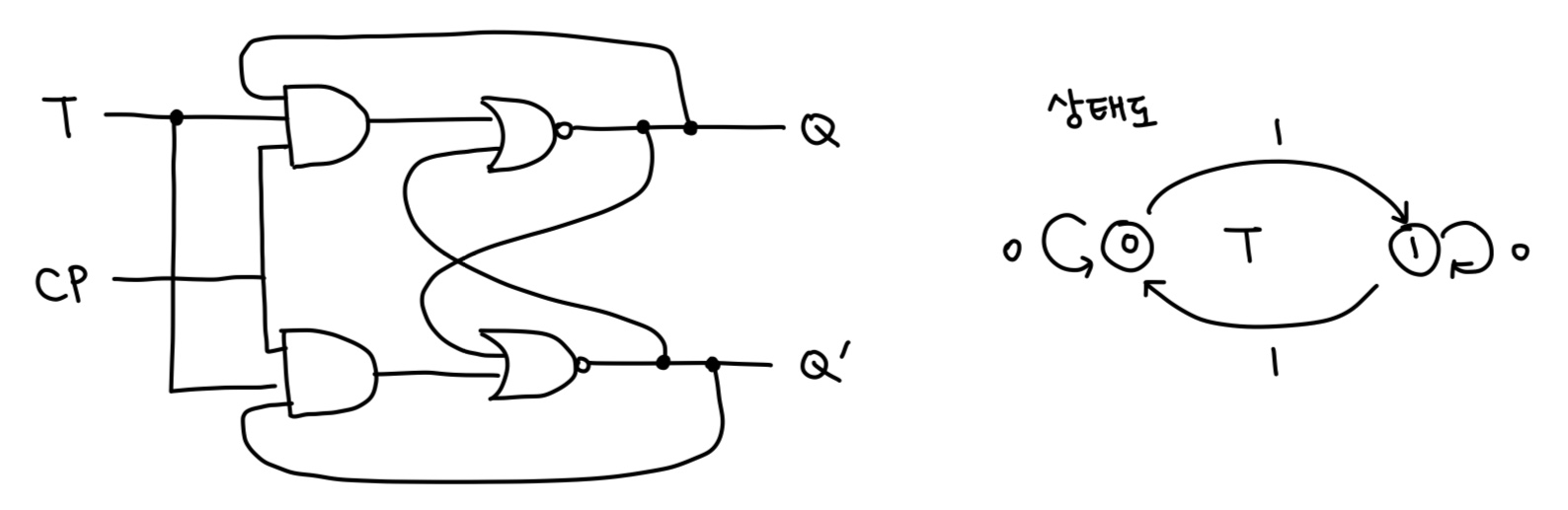
| CP | T | Q |
| 1 | 0 | 불변 |
| 1 | 1 | 반전 |
| 0 | 0 |
728x90
'데이터분석 > CS 기초' 카테고리의 다른 글
| 컴퓨터구조 9-14주차 (0) | 2025.10.18 |
|---|---|
| 이산수학 1-7주차 (2) | 2025.08.29 |
| 자료구조 1-7주차 (0) | 2025.02.21 |
| 알고리즘 1-7주차 (1) | 2025.02.21 |
| C언어(1) 1-7주차 (1) | 2024.12.27 |