Archive
Chapter 2. Preliminaries 본문
728x90
- Network analysis의 technical background를 위한 chapter!
Background on Graphs
basic definitions and concepts
- graph G = (V, E)
- vertices (nodes) V
- order 정점의 수 Nv = |V|
- edges (links) E
- size 간선의 수 Ne = |E|
- vertices (nodes) V
- connectivity
- adjacency
- 두 정점이 간선으로 연결되어 있는 경우
- 두 간선이 공통의 정점 tail을 가지는 경우
- incident on
- 정점과 간선이 연결되어 있는 경우
- 그 개수를 degree dv
- 모든 정점을 degree non-decreasing order로 나열하면 degree sequence
- 모든 정점의 degree 더하면 해당 graph에 있는 간선의 개수의 두 배
- digraph의 경우, 정점으로 들어오는 간선의 개수를 in-degree, 정점에서 나가는 간선의 개수를 out-degree라고 함
- adjacency
- movement
- walk 간선을 따라 이동하는 것
- 이때 지나는 간선의 개수가 length
- 변형
- trail 동일한 간선을 반복하지 않는 walk
- path 동일한 정점을 반복하지 않는 trail
- circuit 시작 정점과 끝 정점이 같은 trail
- cycle 길이가 3이상이며, 시작 정점과 끝 정점이 같은 path
- cycle이 존재하지 않으면 acyclic graph라고 함.
- distance (geodesic distance) 두 정점 사이의 가장 짧은 경로의 길이
- 가장 긴 경로의 길이는 diameter
- walk 간선을 따라 이동하는 것
- 그래프에 숫자 값을 추가하여 정점이나 간선에 의미를 부여할 수 있음
- 간선에 숫자 값을 부여한다면 edge weight
- multi-graph에서 각 정점에 해당 점이 가진 loop의 개수를 labeling하거나 각 간선에 multi-edge의 개수를 labeling하기도 함.
families of graphs
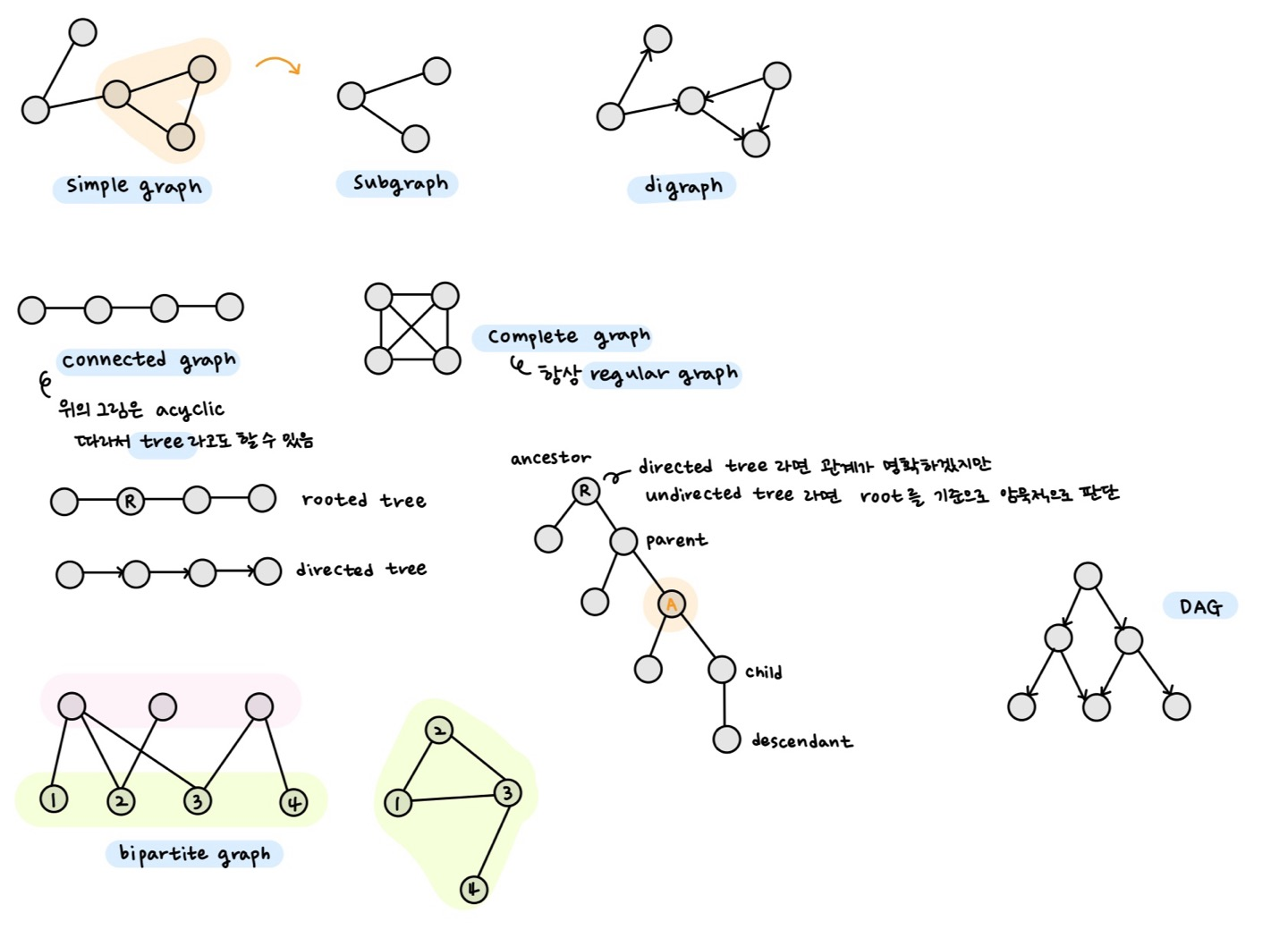
- subgraph H
- H = (Vh, Eh) is a subgraph of G = (Vg, Eg) if Vh ⊆ Vg and Eh ⊆ Eg.
- 원래 그래프에서 특정 vertex set을 선택한 후, 해당 정점들 사이에 존재하는 모든 간선들을 포함하면 induced subgraph
- loop이나 multi-edges 포함하면 multi-graph, 그렇지 않다면 simple graph
- 특별한 언급이 없을 경우 simple graph를 의미한다고 봐도 무관.
- 간선 방향을 구분한다면 directed graph (digraph)
- 이때 방향이 있는 간선을 directed edges (arcs)라고 하고, read from left tail to right head.
- 서로 반대 방향으로 연결된 두 간선들은 said to be mutual
- connected graph
- 모든 정점이 다른 정점에서 reachable
- digraph의 경우, 방향성을 제거했을 때 connected graph가 된다면 weakly connected되었다고 하고, 방향성을 제거하지 않고도 connected graph가 된다면 strongly connected되었다고 함.
- subgraph 중에서 더 이상 간선을 추가할 수 없는 connected graph를 maximally connected subgraph라고 함.
- complete graph
- 모든 정점이 간선으로 서로 연결됨
- 전체 그래프가 complete하지 않아도 일부 정점들끼리 완전히 연결되어 있다면 그 부분을 clique라고 함.
- 그래프 안에서 더 이상 확장할 수 없는 가장 큰 clique는 maximal clique
- regular graph
- 모든 정점이 동일한 degree를 갖는 그래프
- tree
- 사이클이 없는 connected graph
- 방향성이 있다면 directed tree
- 그래프의 모든 다른 정점으로 가는 path가 존재하는 root를 가진다면 rooted tree
- 이러한 tree들의 disjoint union을 forest라고 함.
- directed acyclic graph DAG
- 사이클이 없고 방향성을 가지는 그래프
- 얼핏 tree와 유사한 구조를 가지지만, 방향성만 없애면 사이클이 생길 수 있다는 점이 다름.
- bipartite graph
- 그래프의 정점들은 두 그룹으로 나뉘고, 간선은 항상 다른 그룹의 두 정점을 연결
- bipartite graph 내용을 바탕으로 각 그룹 내 정점들끼리 연결된 그래프를 만든다면 induced graph
- planar graph
- 그래프를 평면에 그릴 때, 간선이 서로 교차하지 않도록 그릴 수 있어야 함
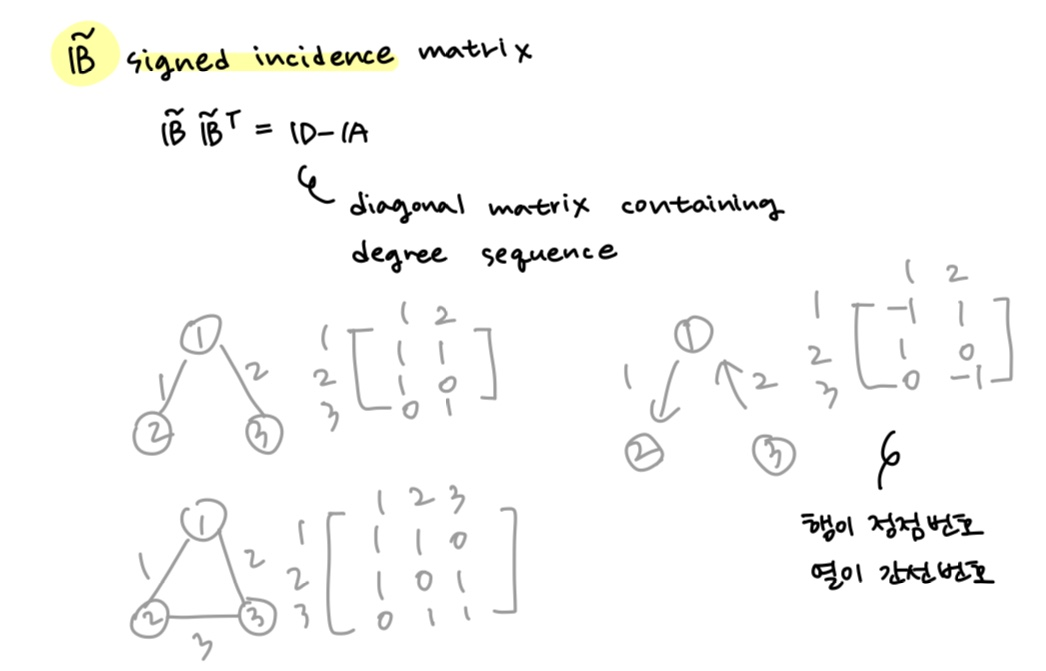
graphs and matrix algebra


graph data structures and algorithms

Background in Probability and Statistics
probability
asymptotic statements
simulation of random variables
principles of statistical inference
methods of statistical inference
network data analysis brief intro



728x90
'통계 > 네트워크분석' 카테고리의 다른 글
| Lab4 (0) | 2025.03.16 |
|---|---|
| Chapter 4. Descriptive Analysis of Network Graph Characteristics (1) | 2025.02.08 |
| Chapter 3. Mapping Networks (1) | 2025.02.02 |
| Chapter 1. Introduction and Overview (1) | 2025.01.26 |