Archive
Chapter 4. Descriptive Analysis of Network Graph Characteristics 본문
728x90
참고: Statistical Analysis of Network Data
- network graph에서 유용한 정 찾는 분석 기법들을 소개하는 chapter!
Introduction
- 네트워크를 두 가지 주요 범주로 나눠 분석할 것!
- characterization of individual vertices and edges (e.g. 이 네트워크에서 가장 중요한 vertex는 무엇인가?)
- characterization of network cohesion (e.g. 이 네트워크에서 community는 어떻게 형성되는가?)
- 위 두 범주는 local과 global의 구분과는 다른 개념, vertex level characteristic이 네트워크 전체를 요약하기도 하고 cohesion among vertices가 그래프 특정 부분만 요약하기도 하기 때문
Vertex and Edge Characteristics
Characteristics based upon vertex degrees
- degree distribution

- e.g. 어떤 그래프의 corresponding degree sequence가 {1, 3, 4, 4, 3, 3}이라면, {f1=1/6, f3=1/2, f4=1/3}가 degree distribution
- 많은 네트워크가 power-law distribution 따름
- 그 여부는 hill plot에서 alpha값 변동성 분석함으로써 확인 가능

- 해석 시 주의할 점은
- 너무 작은 네트워크에서는 분석 결과를 신뢰할 수 없음
- 불가능한 max degree 있을 수 있음
(e.g. internet network에서 개별 router가 연결할 수 있는 node 수는 보통 64~128개. 하지만 분석된 네트워크에서는 1071개의 연결을 가진 node가 존재. 이는 실제로 1071개의 연결을 가진 하나의 router가 존재하는 게 아니라 여러 개의 router가 묶여 나타났을 가능성이 큼) - 해결 방법: 단순한 power-law model이 아니나 power-law + exponential truncation model 사용
- 그 여부는 hill plot에서 alpha값 변동성 분석함으로써 확인 가능
- degree correlation
- degree distribution만으로는 어떤 degree의 vertex들이 서로 연결되어 있는지 확인할 수 없기에 부족,
따라서 다음 세 가지 통계량을 활용! - joint degree distribution
- degree가 어떻게 조합되는지 요약한 분포 (e.g. (d1, d2)가 얼마나 자주 발생하는지 계산)
- undirected graph에서는 (d1, d2)와 (d2, d1)을 동일한 것으로 처리해야 함
- average neighbor degree
- degree가 d인 vertex의 neighbor들의 degree 평균을 계산

- average neighbor degree가 degree 커질수록 감소하면: 높은 degree의 vertex가 낮은 degree의 vertex와 연결되는 경향이 강함
- average neighbor degree가 degree 커질수록 증가하면: 높은 degree의 vertex끼리 서로 연결되는 경향이 강함
- degree가 d인 vertex의 neighbor들의 degree 평균을 계산
- degree correlation
- 상관계수가 음수이면: 높은 degree의 vertex가 낮은 degree의 vertex와 연결되는 경향이 강함
- 상관계수가 양수이면: 높은 degree의 vertex끼리 서로 연결되는 경향이 강함
- degree distribution만으로는 어떤 degree의 vertex들이 서로 연결되어 있는지 확인할 수 없기에 부족,
- 네트워크에서 degree가 어떻게 연결되는지는 단순한 우연이 아니라 네트워크가 가지고 있는 구조적 특성을 반영한 결과일 확률이 높음! 따라서 '왜' 그렇게 연결되었는지 해석하는 게 중요함
Characteristics based upon vertex centrality
- centrality는 네트워크의 각 정점의 importance를 측정하기 위한 척도

- closeness centrality

- 한 노드 v에서 다른 모든 노드 u까지의 geodesic distrance의 합 역수 취한 것
- 다른 노드와의 거리가 짧을수록 중요한 노드라고 보는 것!
- 계산 시간 복잡도 O(|V|^2 log|V| + |V||E|)
- 서로 연결되지 않은 두 노드의 경우 centrality 값이 infinity가 되어 분석이 어렵다는 한계가 있음,
각각의 connected component마다 따로 계산하거나 finite upper limit을 설정하여 해결하곤 함
- betweenness centrality

- sigma(s,t|v)는 노드 s에서 노드 v를 지나 노드 t로 가는 shortest path의 개수
sigma(s, t)는 노드 s에서 노드 t로 가는 shortest path의 개수 - 자주 지나가는 노드일수록 중요한 노드라고 보는 것!
- 계산 시간 복잡도 O(|V|^3), 너무 느려서 O(|V| + |E|)까지 개선한듯?
- sigma(s,t|v)는 노드 s에서 노드 v를 지나 노드 t로 가는 shortest path의 개수
- eigenvector centrality

- adjacency matrix의 eigen vector 구하는 방법으로 변환해 계산

- 계산 시간 복잡도 O(|V|^2) per iteration, roughly on par with 나머지 둘 ... 뭐 비슷한 수준이다~
- adjacency matrix의 eigen vector 구하는 방법으로 변환해 계산
Characteristics based on edges
- There are contexts where edges arguably are of greater concern than the vertices
- betweenness centrality는 edge 위주로 쉽게 확장할 수 있지만, 다른 centrality들은 바로 적용하기 어려움
해결 방법은 node를 edge로, edge를 node로 변환하는 daul graph를 만들어 분석하는 방법
Characterizing Network Cohesion
Local Density
- clique 개수 확인
- |E| > (|V|^2/2)(n-2/n-1) 이런 조건을 만족해야 네트워크가 촘촘하고 clique 많아진다는데, real-world 네트워크 보면 대부분 |E| ~ |V| 이라는 점이 문제
- 크기 n 이상인 clique 존재하는지 확인하는 문제 NP-complete인 것도 문제
- 대신 weekend version of this idea 활용하곤 함
- plexes 개수 확인 (m개의 vertices 가진 subgraph가 n-plex라고 하면 no vertex has degree less than m-n)
- cores 개수 확인 (k-core of a graph라고 하면 all vertices have degree 최소 k)
- 대신 weekend version of this idea 활용하곤 함
- 밀도를 직접 계산
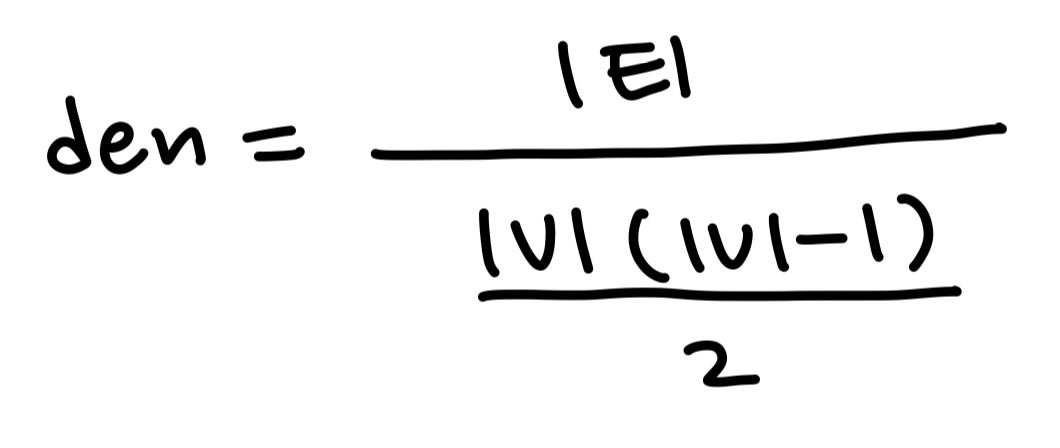
- 친구의 친구가 친구일 확률 나타내는 clustering coefficient 활용
- local clustering coefficient
- global clustering coefficient
728x90
'통계 > 네트워크분석' 카테고리의 다른 글
| Lab4 (0) | 2025.03.16 |
|---|---|
| Chapter 3. Mapping Networks (0) | 2025.02.02 |
| Chapter 2. Preliminaries (0) | 2025.01.26 |
| Chapter 1. Introduction and Overview (0) | 2025.01.26 |